
A preprint of my most recent paper, submitted to the Journal of Differential Equations for peer review: On the stability of Rotating States in Second-Order Self-Propelled Multi-Particle Systems
My Trident Paper: Stability of Nonlinear Swarms on Flat and Curved Surfaces
My Honors Paper: Limit Behavior of Swarms of Coupled Agents
My collaboration with the Naval Research Lab: The Dynamics of Interacting Swarms
In 2018, I presented my work at the Trident Scholar Conference. You can watch my presentation below:
That year, I also presented at the University of Maryland’s Graduate Mathematics Seminar, and the Service Academy Student Mathematics Conference at the US Coast Guard Academy.

SASMC 2018. I’m in the middle row on the right.
My poster at the Trident poster session.
In 2017, I received the Trident Scholarship from the Naval Academy. The Trident Scholarship allowed me to devote 24 credit-hours (total) towards research. My advisor, Prof Kostya Medynets, and I chose to look at mathematical swarm models. In particular, we were interested in the parabolic potential model, a model for swarms based on spring-like attraction. In a system of \(N\) agents, each of which has position vector \(r_i\), the parabolic potential model has the following equation of motion:
\[\ddot{r}_i=(1-\lvert\dot{r}_i\rvert^2)\dot{r}_i-(r_i-R)\]where \(R\) is the center of mass of the system, given by
\[R=\sum_{i=1}^Nr_i\]Expected limit behavior is pictured below:
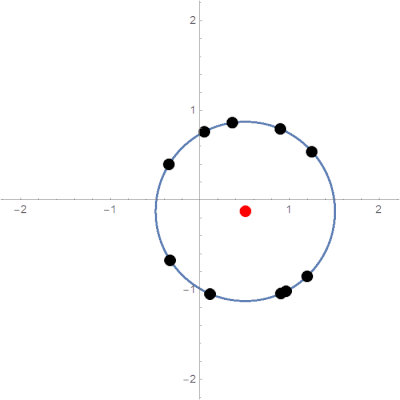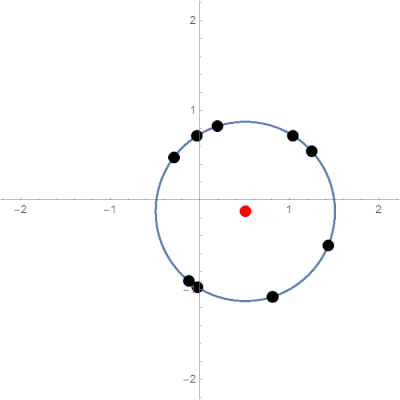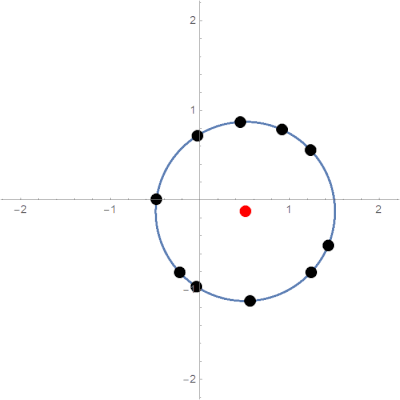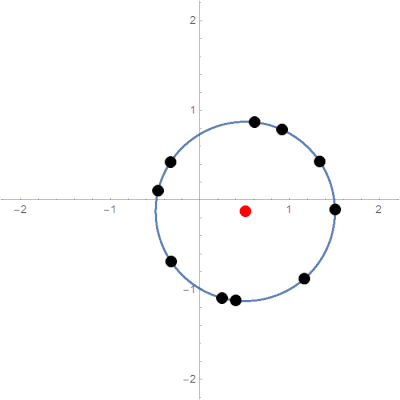
Typical limit behavior of the parabolic potential model.
Over the course of a year, we proved several new results about the stability of this system. We were fortunate to observe some behavior that has never been seen before.
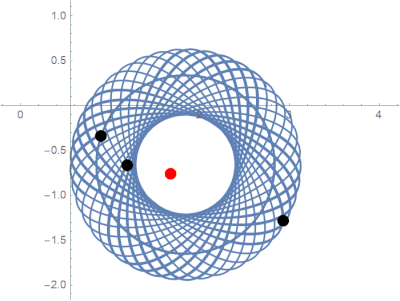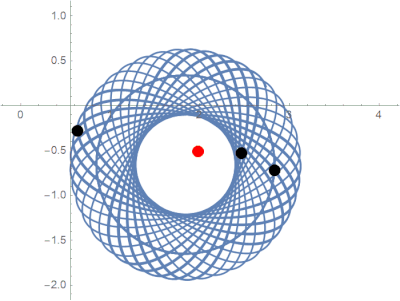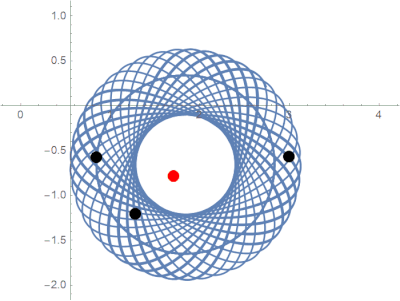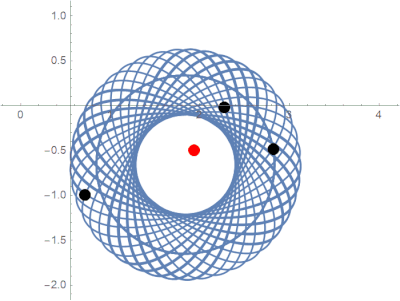
Previously unobserved limit behavior in the parabolic potential model.
Prof Medynets has his own website, which you can see here.
In summer 2017, I interned at the Naval Research Laboratory in Washington, DC, advised by Dr. Ira Schwartz. I researched swarm collisions in systems subject to delay. We summarized our findings in a report, titled The Dynamics of Interacting Swarms, published by the Defense Technical Information Center.
In the course of my work on swarming, I researched applications to unmanned systems. I spent some time getting differential equation models (simulated in Wolfram Mathematica) to drive virtual drones (simulated in Gazebo) using ROS, the Robot Operating System to interface between the two. A video of my work is available on Youtube:
In 2018, I received the Julian Clancy Frazier Award for excellence in Mathematics.